 |
|
МЕНЮ
|
Курсовая работа: Построение неполной квадратичной регрессионной модели по результатам полного факторного экспериментаКоэффициенты уравнения регрессии (6) рассчитываются по зависимости:
где u - номер опыта; Распишем уравнение (7) для всех коэффициентов, входящих в регрессионную модель (6):
Для расчета коэффициентов регрессии составим расширенную матрицу планирования (табл. 5). Таблица 5 Расширенная матрица плана 23
Рассчитаем коэффициенты в уравнении регрессии (6) по зависимостям (8) с учетом знаков Хi в столбцах табл. 5:
Таким образом, получены следующие значения коэффициентов уравнения регрессии: b0 = 111,9; b12 = b4 = -13,14; b1 = -11,03; b13 = b5 = 1,83; b2 = 34,5; b23 = b6 = 4,13; b3 = -0,7125; b123 = b7 = 14,89. Если ввести обозначения b12 = b4; b13 = b5; b23 = b6; b123 = b7 и учесть обозначения, принятые в табл. 5, регрессионное уравнение (6) запишется в виде: y = b0 + b1X1 + b2X2 + b3X3 + b4X4 + b5X5 + b6X6 + b7X7. (9) 5. Проверка статистической значимости коэффициентов регрессии Коэффициенты регрессии, рассчитанные по уравнению (7), строго
говоря, определены не точно, а с некоторой погрешностью. Мерой этой погрешности
является дисперсия оценок коэффициентов. Неизбежное наличие погрешности
в определении коэффициентов регрессии обусловлено колебаниями значений функции
отклика при дублировании экспериментов в каждом опыте. С учетом этого уравнение
(7) можно записать в следующем виде: Поскольку дублирование экспериментов равномерное, дисперсию оценок коэффициентов уравнения регрессии можно рассчитать по зависимости:
где nu – количество дублей в каждом опыте (nu
= 3); N – количество опытов (N = 8); Если ряд дисперсий однороден, средняя дисперсия эксперимента рассчитывается по уравнению:
где Если ряд дисперсий неоднороден (значения функции отклика в разных
опытах определены с различной точностью), но в результатах измерений значений
функции отклика отсутствуют грубые ошибки и промахи, в качестве средней
дисперсии эксперимента принимается максимальная построчная дисперсия. В
соответствии с данными табл. 4 максимальная построчная дисперсия получена в
первом опыте: Среднеквадратичная ошибка |
Copyright © 2012 г.
При использовании материалов - ссылка на сайт обязательна.
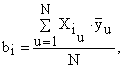 (7)
(7)
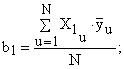
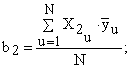
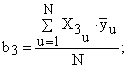 (8)
(8)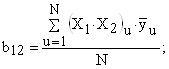
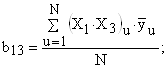
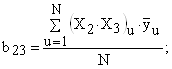

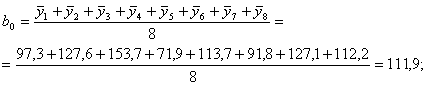

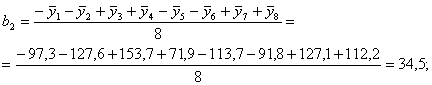
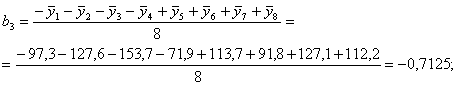
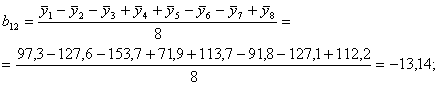



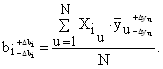 Очевидно, что при достаточно
малых значениях коэффициентов bi абсолютная погрешность их
определения 2×Dbi,
обусловленная погрешностью определения значений функции отклика, может оказаться
недопустимо большой. В этом случае значение коэффициента следует признать
статистически незначимым, а сам коэффициент исключить из регрессионной модели.
Статистическая незначимость коэффициента означает отсутствие его влияния на
исследуемый процесс.
Очевидно, что при достаточно
малых значениях коэффициентов bi абсолютная погрешность их
определения 2×Dbi,
обусловленная погрешностью определения значений функции отклика, может оказаться
недопустимо большой. В этом случае значение коэффициента следует признать
статистически незначимым, а сам коэффициент исключить из регрессионной модели.
Статистическая незначимость коэффициента означает отсутствие его влияния на
исследуемый процесс.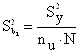 , (10)
, (10)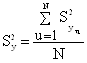 , (11)
, (11)