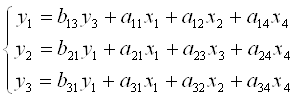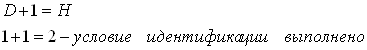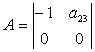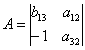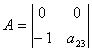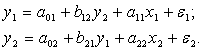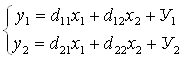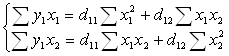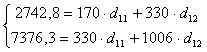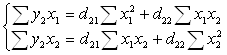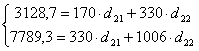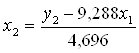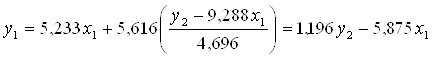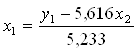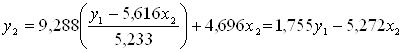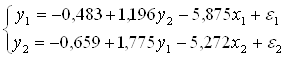Контрольная работа: Уравнения линейной регрессии

Определитель не равен 0, ранг матрицы равен 2, достаточное условие идентификации выполняется. 2-е уравнение точно идентифицируемо.

3) В 3-м уравнении 2 эндогенные переменные y2, y3 (Н=2); отсутствует 1 экзогенная х4 (D=1).

1+1=2 — необходимое условие идентификации выполняется.

Составим матрицу из коэффициентов при отсутствующих переменных.

Определитель не равен 0, ранг матрицы равен 2-м, достаточное условие идентификации выполняется. 3-е уравнение точно идентифицируемо.

Т.о, если все 3 уравнения идентифицируемы, то и СФМ идентифицируема.

б) СФМ имеет вид:

Проверим систему на идентифицируемость, для этого проверим каждое уравнение на выполнение необходимого и достаточного условия идентификации.

1) В 1-м уравнении 2 эндогенных переменных y1, y3 (Н=2); отсутствующая экзогенная переменная х3 (D=1).

Составим матрицу из коэффициентов при отсутствующих переменных.

Достаточное условие не выполнено, уравнение не идентифицируемо.

2) Во 2-м уравнении 2 эндогенных переменных y1, y2 (Н=2). Отсутствующая экзогенная переменная х2 (D=1). Необходимое условие D+1=H выполняется.

Составим матрицу из коэффициентов при отсутствующих переменных.

Необходимое условие идентификации выполняется. 2-е уравнение точно идентифицируемо.

3) В 3-м уравнении 2 эндогенных переменных y1, y3 (Н=2); отсутствующая экзогенная переменная х3 (D=1). Необходимое условие D+1=H выполняется. Составим матрицу из коэффициентов при отсутствующих переменных.

Достаточное условие не выполняется. 3-е уравнение не идентифицируемо.

Т.к. 1-е и 3-е уравнения не идентифицируемы, то и вся СФМ не является идентифицируемой.

Ответ: а) СФМ идентифицируема; б) СФМ не является идентифицируемой.

Задача 2 в

По данным таблицы для своего варианта, используя косвенный метод наименьших квадратов, построить структурную форму модели вида:

Табл. 2.2.

Решение

Структурную модель преобразуем в приведенную форму модели.

Для нахождения коэффициентов первого приведенного уравнения используем систему нормальных уравнений.

Расчеты произведем в табл. 2.3.

Табл. 2.3.

Подставив полученные значения в систему нормальных уравнений.

Решение этих уравнений дает значения d11=5,233; d12=5,616.

1-e уравнение ПФМ имеет вид:

Для нахождения коэффициентов d2k второго приведенного уравнения используем следующую систему нормальных уравнений

Расчеты произведем в табл. 2.3.

Подставив полученные значения в систему нормальных уравнений, получим

Решение этой системы дает значения d21=9,288; d22=4,696.

2-е уравнение ПФМ имеет вид

Для перехода от ПФМ к СФМ найдем х2 из второго уравнения.

Подставив это выражение в 1-е уравнение, найдем структурное уравнение.

т.о. b12=1,196; a11=-5,875.

Найдем х1 из 1-го уравнения ПФМ

Подставив это выражение во 2-е уравнение ПФМ, найдем структурное уравнение.

т.о. b21=1,775; a22=-5,272

Свободные члены СФМ находим из уравнений

линейный регрессия детерминация аппроксимация квадрат

Ответ: окончательный вид СФМ таков