 |
|
МЕНЮ
|
Реферат: Управление техническими системами (лекции)
где
Линеаризация
ДУ происходит аналогично, отличие состоит только в том, что необходимо искать
частные производные по производным ( Пример. Линеаризация нелинейного ДУ. 3xy - 4x2 + 1,5 Данное
ДУ является нелинейным из-за наличия произведений переменных х и у.
Линеаризируем его в окрестности точки с координатами х0 = 1, 3у0 - 4 + 0 = 0 + у0 откуда у0 = 2. Введем в рассмотрение функцию F = 3xy - 4x2 + 1,5x’y - 5y’ - y и определим все ее производные при заданных начальных условиях:
Теперь, используя полученные коэффициенты, можно записать окончательное линейное ДУ: -5.Dy’ + 2.Dy + 3.Dх’ - 2.Dх = 0. ¨ 2.5. Преобразования Лапласа. Исследование АСР существенно упрощается при использовании прикладных математических методов операционного исчисления. Например, функционирование некоторой системы описывается ДУ вида где х и у - входная и выходная величины. Если в данное уравнение вместо x(t) и y(t) подставить функции X(s) и Y(s) комплексного переменного s такие, что то исходное ДУ при нулевых начальных условиях равносильно линейному алгебраическому уравнению a2 s2 Y(s) + a1 s Y(s) + a0 Y(s) = b1 X(s) + b0 X(s). Такой переход от ДУ к алгебраическому уравнению называется преобразованием Лапласа, формулы (2.2) соответственно формулами преобразования Лапласа, а полученное уравнение - операторным уравнением. Новые функции X(s) и Y(s) называются изображениями x(t) и y(t) по Лапласу, тогда как x(t) и y(t) являются оригиналами по отношению к X(s) и Y(s). Переход
от одной модели к другой достаточно прост и заключается в замене знаков
дифференциалов Для обратного перехода от операторного уравнения к функциям от времени используется метод обратного преобразования Лапласа. Общая формула обратного преобразования Лапласа:
где f(t) - оригинал, F(jw) - изображение при s = jw, j - мнимая единица, w - частота. Эта формула достаточно сложна, поэтому были разработаны специальные таблицы (см. табл. 1.1 и 1.2), в которые сведены наиболее часто встречающиеся функции F(s) и их оригиналы f(t). Они позволяют отказаться от прямого использования формулы (2.3). Таблица 1.2 - Преобразования Лапласа
Таблица 1.2 - Формулы обратного преобразования Лапласа (дополнение)
Закон изменения выходного сигнала обычно является функцией, которую необходимо найти, а входной сигнал, как правило, известен. Некоторые типовые входные сигналы были рассмотрены в п. 2.3. Здесь приводятся их изображения: единичное
ступенчатое воздействие имеет изображение X(s) = дельта-функция X(s) = 1, линейное
воздействие X(s) = Пример. Решение ДУ с использованием преобразований Лапласа.
Допустим,
входной сигнал имеет форму единичного ступенчатого воздействия, т.е. x(t) =
1. Тогда изображение входного сигнала X(s) = Производим преобразование исходного ДУ по Лапласу и подставляем X(s): s2Y + 5sY + 6Y = 2sX + 12X, s2Y + 5sY + 6Y = 2s Y(s3 + 5s2 + 6s) = 2s + 12. Определяется выражение для Y:
Оригинал полученной функции отсутствует в таблице оригиналов и изображений. Для решения задачи его поиска дробь разбивается на сумму простых дробей с учетом того, что знаменатель может быть представлен в виде s(s + 2)(s + 3):
= Сравнивая получившуюся дробь с исходной, можно составить систему из трех уравнений с тремя неизвестными:
5.М1 + 3.М2 + 2.М3 = 2 à M2 = -4 6.М1 = 12 M3 = 2 Следовательно, дробь можно представить как сумму трех дробей:
Теперь, используя табличные функции, определяется оригинал выходной функции: y(t) = 2 - 4.e-2t + 2.e-3t. ¨ 2.6. Передаточные функции. 2.6.1 Определение передаточной функции. Преобразование ДУ по Лапласу дает возможность ввести удобное понятие передаточной функции, характеризующей динамические свойства системы. Например, операторное уравнение 3s2Y(s) + 4sY(s) + Y(s) = 2sX(s) + 4X(s) можно преобразовать, вынеся X(s) и Y(s) за скобки и поделив друг на друга: Y(s)*(3s2 + 4s + 1) = X(s)*(2s + 4)
Полученное выражение называется передаточной функцией. Передаточной функцией называется отношение изображения выходного воздействия Y(s) к изображению входного X(s) при нулевых начальных условиях.
Передаточная функция является дробно-рациональной функцией комплексной переменной:
где B(s) = b0 + b1s + b2 s2 + … + bm sm - полином числителя, А(s) = a0 + a1s + a2 s2 + … + an sn - полином знаменателя. Передаточная функция имеет порядок, который определяется порядком полинома знаменателя (n). Из (2.4) следует, что изображение выходного сигнала можно найти как Y(s) = W(s)*X(s). Так как передаточная функция системы полностью определяет ее динамические свойства, то первоначальная задача расчета АСР сводится к определению ее передаточной функции. 2.6.2 Примеры типовых звеньев. Звеном системы называется ее элемент, обладающий определенными свойствами в динамическом отношении. Звенья систем регулирования могут иметь разную физическую основу (электрические, пневматические, механические и др. звенья), но относится к одной группе. Соотношение входных и выходных сигналов в звеньях одной группы описываются одинаковыми передаточными функциями. Простейшие типовые звенья: · усилительное, · интегрирующее, · дифференцирующее, · апериодическое, · колебательное, · запаздывающее. 1) Усилительное звено.
Выходной сигнал такого звена в точности повторяет входной сигнал, усиленный в К раз (см. рис. 1.15). Примерами таких звеньев являются: механические передачи, датчики, безынерционные усилители и др. 2) Интегрирующее. 2.1) Идеальное интегрирующее. Выходная величина идеального интегрирующего звена пропорциональна интегралу входной величины.
При подаче на вход звена воздействия выходной сигнал постоянно возрастает (см. рис. 1.16). Это звено астатическое, т.е. не имеет установившегося режима. 2.2) Реальное интегрирующее.
W(s) = Переходная характеристика в отличие от идеального звена является кривой (см. рис. 1.17). Примером интегрирующего звена является двигатель постоянного тока с независимым возбуждением, если в качестве входного воздействия принять напряжение питания статора, а выходного - угол поворота ротора. 3) Дифференцирующее. 3.1) Идеальное дифференцирующее. Выходная величина пропорциональна производной по времени от входной:
При ступенчатом входном сигнале выходной сигнал представляет собой импульс (d-функцию). 3.2) Реальное дифференцирующее.
W(s) = 4) Апериодическое (инерционное). Этому звену соответствуют ДУ и ПФ вида:
Определим характер изменения выходной величины этого звена при подаче на вход ступенчатого воздействия величины х0. Изображение ступенчатого воздействия: X(s) = Y(s) = W(s) X(s) = Разложим дробь на простые: Оригинал первой дроби по таблице: L-1{ L-1{ Тогда окончательно получаем:
Постоянная Т называется постоянной времени. Большинство тепловых объектов являются апериодическими звеньями. Например, при подаче на вход электрической печи напряжения ее температура будет изменяться по аналогичному закону (см. рис. 1.19). 5) Колебательное звено имеет ДУ и ПФ вида
W(s) = При подаче на вход ступенчатого воздействия амплитудой х0 на переходная кривая будет иметь один из двух видов: апериодический (при Т1 ³ 2Т2) или колебательный (при Т1 < 2Т2). 6) Запаздывающее. y(t) = x(t - t), W(s) = e-ts. Выходная величина у в точности повторяет входную величину х с некоторым запаздыванием t. Примеры: движение груза по конвейеру, движение жидкости по трубопроводу. 2.6.3 Соединения звеньев. Поскольку исследуемый объект в целях упрощения анализа функционирования разбит нами на звенья, то после определения передаточных функций для каждого звена встает задача объединения их в одну передаточную функцию объекта. Вид передаточной функции объекта зависит от последовательности соединения звеньев:
Wоб = W1.W2.W3… При последовательном соединении звеньев их передаточные функции перемножаются. 2) Параллельное соединение.
При параллельном соединении звеньев их передаточные функции складываются.
Передаточная функция по заданию (х):
«+» соответствует отрицательной ОС, «-» - положительной. Для определения передаточных функций объектов, имеющих более сложные соединения звеньев, используют либо последовательное укрупнение схемы, либо преобразуют по формуле Мезона. 2.6.4 Передаточные функции АСР.
Это необходимо, во-первых, для того, чтобы определить математические зависимости в системе, и, во-вторых, как правило, все инженерные методы расчета и определения параметров настройки регуляторов применены для такой стандартной структуры. В общем случае любая одномерная АСР с главной обратной связью путем постепенного укрупнения звеньев может быть приведена к такому виду. Если выход системы у не подавать на ее вход, то мы получим разомкнутую систему регулирования, передаточная функция которой определяется как произведение: W¥ = Wp.Wy (Wp - ПФ регулятора, Wy - ПФ объекта управления).
Фз(s) = (далее будем рассматривать только системы с обратной отрицательной связью, поскольку они используются в подавляющем большинстве АСР). Данная передаточная функция Фз(s) определяет зависимость у от х и называется передаточной функцией замкнутой системы по каналу задающего воздействия (по заданию). |
|||||||||||||||||||||||||||||||||
Copyright © 2012 г.
При использовании материалов - ссылка на сайт обязательна.
 Графически
линеаризацию некоторого уравнения от двух переменных F(х,у) = 0 в
окрестности некоторой точки (х0, у0) можно представить
как замену рассматриваемого участка кривой на касательную (см. рис. 1.14),
уравнение которой определяется по формуле:
Графически
линеаризацию некоторого уравнения от двух переменных F(х,у) = 0 в
окрестности некоторой точки (х0, у0) можно представить
как замену рассматриваемого участка кривой на касательную (см. рис. 1.14),
уравнение которой определяется по формуле: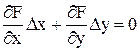 ,
,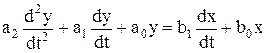 , (2.1)
, (2.1)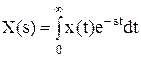 и
и 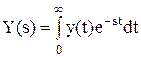 , (2.2)
, (2.2)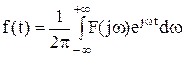 , (2.3)
, (2.3)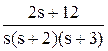 =
=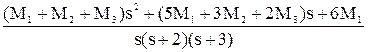 .
.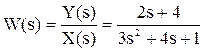 .
.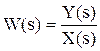 (2.4)
(2.4)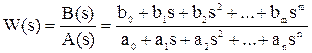 ,
, Звено
усиливает входной сигнал в К раз. Уравнение звена у = К*х, передаточная функция
W(s) = К. Параметр К называется коэффициентом усиления.
Звено
усиливает входной сигнал в К раз. Уравнение звена у = К*х, передаточная функция
W(s) = К. Параметр К называется коэффициентом усиления.

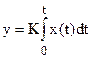 ; W(s) =
; W(s) =  Передаточная
функция этого звена имеет вид:
Передаточная
функция этого звена имеет вид: 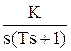 .
. Идеальные
дифференцирующие звенья физически не реализуемы. Большинство объектов, которые
представляют собой дифференцирующие звенья, относятся к реальным
дифференцирующим звеньям. Переходная характеристика и передаточная функция
этого звена имеют вид:
Идеальные
дифференцирующие звенья физически не реализуемы. Большинство объектов, которые
представляют собой дифференцирующие звенья, относятся к реальным
дифференцирующим звеньям. Переходная характеристика и передаточная функция
этого звена имеют вид: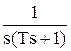 .
.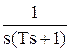 =
=
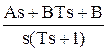 =
=  y(t) = K x0 (1 -
y(t) = K x0 (1 - 
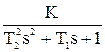 .
. 1) Последовательное соединение.
1) Последовательное соединение.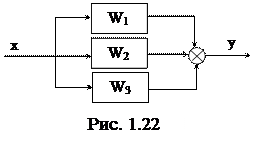 Wоб = W1 + W2 + W3 + …
Wоб = W1 + W2 + W3 + …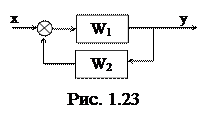 3) Обратная связь
3) Обратная связь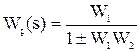
 Для
исследования и расчета структурную схему АСР путем эквивалентных преобразований
приводят к простейшему стандартному виду «объект - регулятор».
Для
исследования и расчета структурную схему АСР путем эквивалентных преобразований
приводят к простейшему стандартному виду «объект - регулятор». То
есть последовательность звеньев Wp и
Wy может быть заменена одним звеном с W¥. Передаточную функцию замкнутой системы принято
обозначать как Ф(s). Она может быть выражена через W¥:
То
есть последовательность звеньев Wp и
Wy может быть заменена одним звеном с W¥. Передаточную функцию замкнутой системы принято
обозначать как Ф(s). Она может быть выражена через W¥: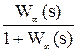 .
.