 |
|
МЕНЮ
|
Реферат: Управление техническими системами (лекции)Для АСР существуют также передаточные функции по другим каналам: Фe(s) = Фв(s) = Поскольку
передаточная функция разомкнутой системы является в общем случае
дробно-рациональной функцией вида W¥ = Фз(s) = Как видно, эти передаточные функции отличаются только выражения ми числителей. Выражение знаменателя называется характеристическим выражением замкнутой системы и обозначается как Dз(s) = A(s) + B(s), в то время как выражение, находящееся в числителе передаточной функции разомкнутой системы W¥, называется характеристическим выражением разомкнутой системы B(s).
2.6.5 Определение параметров передаточной функции объекта по переходной кривой. Процесс получения передаточной функции объекта, исходя из данных о переходном процессе, называется идентификацией объекта. Предположим, что при подаче на вход некоторого объекта ступенчатого воздействия была получена переходная характеристика (см. рис. 1.26). Требуется определить вид и параметры передаточной функции.
(инерционной звено с запаздыванием). Параметры передаточной функции: К - коэффициент усиления, Т - постоянная времени, t - запаздывание. Коэффициентом усиления называется величина, показывающая, во сколько раз данное звено усиливает входной сигнал (в установившемся режиме), и равна отношению выходной величины у в установившемся режиме ко входной величине х:
Установившееся значение выходной величины ууст - это значение у при t ® ¥. Запаздыванием t называется промежуток времени от момента изменения входной величины х до начала изменения выходной величины у. Постоянная времени Т может быть определена несколькими методами в зависимости от вида передаточной функции. Для рассматриваемой передаточной функции 1-го порядка Т определяется наиболее просто: сначала проводится касательная к точке перегиба, затем находятся точки пересечения с осью времени и асимптотой yуст; время Т определяется как интервал времени между этими точками. В случае, если на графике между точкой перегиба имеется вогнутость, определяется дополнительное запаздывание tдоп, которое прибавляется к основному: t = t + tдоп. 2.7. Частотные характеристики. 2.7.1 Определение частотных характеристик. Известно, что динамические процессы могут быть представлены частотными характеристиками (ЧХ) путем разложения функции в ряд Фурье. Предположим, имеется некоторый объект и требуется определить его ЧХ. При экспериментальном снятии ЧХ на вход объекта подается синусоидальный сигнал с амплитудой Авх = 1 и некоторой частотой w, т.е.
Тогда после прохождения переходных процессов на выходе мы будем также иметь синусоидальный сигналтой же частоты w, но другой амплитуды Авых и фазы j: у(t) = Авыхsin(wt + j) При разных значениях w величины Авых и j, как правило, также будут различными. Эта зависимость амплитуды и фазы от частоты называется частотной характеристикой. Виды ЧХ: ·
· АЧХ - зависимость амплитуды от частоты; · ФЧХ - зависимость фазы от частоты; · ЛАХ, ЛАЧХ - логарифмические АЧХ. На комплексной плоскости входная величина x = Авх.sin(wt) для каждого момента времени ti определяется вектором х на комплексной плоскости. Этот вектор имеет длину, равную Авх, и отложен под углом wti к действительной оси. (Re - действительная ось, Im - мнимая ось) Тогда величину х можно записать в комплексной форме х(t) = Авх(cos(wt) + j.sin(wt)), где
j = Или, если использовать формулу Эйлера eja = cosa + j.sina, то можно записать х(t) = Авх.ejwt. Выходной сигнал y(t) можно аналогично представить как вектор y(t) = Авых.ej(wt+j). Рассмотрим связь передаточной функции и частотной характеристики. Определим производные по Лапласу: у ® Y у’ ® sY у” ® s2Y и т.д. Определим производные ЧХ: у’(t) = jw Авыхеj(wt + j) = jw у, у”(t) = (jw)2 Авыхеj(wt + j) = (jw)2 у и т.д. Отсюда видно соответствие s = jw. Вывод: частотные характеристики могут быть построены по передаточным функциям путем замены s = jw. Пример:
При s = jw имеем:
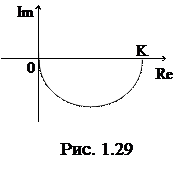
= Изменяя w от 0 до ¥, можно построить АФХ (см. рис.). ¨
Формулы получения АФХ по АЧХ и ФЧХ: Re(w) = A(w) cos j(w), Im(w) = A(w) sin j(w). 2.7.2 Логарифмические частотные характеристики. Логарифмические частотные характеристики (ЛЧХ) используются довольно часто для описания динамических параметров различных устройств. Существуют два основных вида ЛЧХ, которые, как правило, используются совместно и изображаются в виде графиков: 1) ЛАЧХ - логарифмическая АЧХ.
Единица измерения - децибел (дБ). На графике ЛАЧХ по оси абсцисс откладывается частота в логарифмическом масштабе. Это означает, что равным величинам отрезков по оси w соответствуют кратные значения частоты. Для ЛЧХ кратность = 10. По оси ординат откладываются значения L(w) в обычном масштабе. 2) ЛФЧХ - логарифмическая ФЧХ. Представляет из себя ФЧХ, у которой ось частоты w проградуирована в логарифмическом масштабе в соответствии с ЛАЧХ. По оси ординат откладываются фазы j. Примеры ЛЧХ. 1. Фильтр низких частот (ФНЧ)
Фильтр низких частот предназначен для подавления высокочастотных воздействий. 2. Фильтр высоких частот (ФВЧ)
Фильтр высоких частот предназначен для подавления низкочастотных воздействий. 3. Заградительный фильтр. Заградительный фильтр подавляет только определенный диапазон частот ЛАЧХ и ЛФЧХ Пример цепи
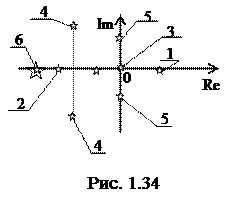
. 3. Качество процессов управления. 3.1. Критерии устойчивости. 3.1.1 Устойчивость. Важным показателем АСР является устойчивость, поскольку основное ее назначение заключается в поддержании заданного постоянного значения регулируемого параметра или изменение его по определенному закону. При отклонении регулируемого параметра от заданной величины (например, под действием возмущения или изменения задания) регулятор воздействует на систему таким образом, чтобы ликвидировать это отклонение. Если система в результате этого воздействия возвращается в исходное состояние или переходит в другое равновесное состояние, то такая система называется устойчивой. Если же возникают колебания со все возрастающей амплитудой или происходит монотонное увеличение ошибки е, то система называется неустойчивой. Для того, чтобы определить, устойчива система или нет, используются критерии устойчивости: 1) корневой критерий, 2) критерий Стодолы, 3) критерий Гурвица, 4) критерий Найквиста, 5) критерий Михайлова и др. Первые два критерия являются необходимыми критериями устойчивости отдельных звеньев и разомкнутых систем. Критерий Гурвица является алгебраическим и разработан для определения устойчивости замкнутых систем без запаздывания. Последние два критерия относятся к группе частотных критериев, поскольку определяют устойчивость замкнутых систем по их частотным характеристикам. Их особенностью является возможность применения к замкнутым системам с запаздыванием, которыми является подавляющее большинство систем управления. 3.1.2 Корневой критерий. Корневой критерий определяет устойчивость системы по виду передаточной функции. Динамической характеристикой системы, описывающей основные поведенческие свойства, является характеристический полином, находящийся в знаменателе передаточной функции. Путем приравнивания знаменателя к нулю можно получить характеристическое уравнение, по корням которого определить устойчивость. Корни характеристического уравнения могут быть как действительные, так и комплексные и для определения устойчивости откладываются на комплексной плоскости (см. рис. 1.34).
- Действительные: положительные (корень № 1); отрицательные (2); нулевые (3); - Комплексные комплексные сопряженные (4); чисто мнимые (5); По кратности корни бывают: одиночные (1, 2, 3); сопряженные (4, 5): si = a ± jw; кратные (6) si = si+1 = … Корневой критерий формулируется следующим образом: Линейная АСР устойчива, если все корни характеристического уравнения лежат в левой полуплоскости. Если хотя бы один корень находится на мнимой оси, которая является границей устойчивости, то говорят, что система находится на границе устойчивости. Если хотя бы один корень находится в правой полуплоскости (не зависимо от числа корней в левой), то система является неустойчивой. Иными словами, все действительные корни и действительные части комплексных корней должны быть отрицательны. В противном случае система неустойчива. Пример 3.1. Передаточная функция системы имеет вид:
Характеристическое уравнение: s3 + 2s2 + 2.25s + 1.25 = 0. Корни: s1 = -1; s2 = -0,5 + j; s3 = -0,5 - j. Следовательно, система устойчива. ¨ 3.1.3 Критерий Стодолы. Этот критерий является следствием из предыдущего и формулируется следующим образом: Линейная система устойчива, если все коэффициенты характеристического полинома положительны. То есть, для передаточная из примера 3.1 по критерию Стодола соответствует устойчивой системе. 3.1.4 Критерий Гурвица. Критерий Гурвица работает с характеристическим полиномом замкнутой системы. Как известно, структурная схема АСР по ошибке имеет вид (см. рис.) Wp - передаточная функция регулятора,
Определим передаточную функцию для прямой связи (передаточную функцию разомкнутой системы, см. п. 2.6.4): W¥ = Wp Wy. Далее с учетом наличия отрицательной обратной связи получаем передаточную функцию замкнутой системы:
Как правило, передаточная функция разомкнутой системы имеет дробно-рациональный вид:
Тогда после подстановки и преобразования получаем:
Отсюда следует, что характеристический полином замкнутой системы (ХПЗС) можно определить как сумму числителя и знаменателя W¥: Dз(s) = A(s) + B(s). Для определения устойчивости по Гурвицу строится матрица таким образом, чтобы по главной диагонали были расположены коэффициенты ХПЗС с an+1 по a0. Справа и слева от нее записываются коэффициенты с индексами через 2 (a0, a2, a4… или a1, a3, a5 …). Тогда для устойчивой системы необходимо и достаточно, чтобы определитель и все главные диагональные миноры матрицы были больше нуля. Если хотя бы один определитель будет равен нулю, то система будет находится на границе устойчивости. Если хотя бы один определитель будет отрицателен, то система неустойчива не зависимо от числа положительных или нулевых определителей. Пример. Дана передаточная функция разомкнутой системы
Требуется определить устойчивость замкнутой системы по критерию Гурвица. Для этого определяется ХПЗС: D(s) = A(s) + B(s) = 2s4 + 3s3 + s2 + 2s3 + 9s2 + 6s + 1 = 2s4 + 5s3 + 10s2 + 6s + 1. Поскольку степень ХПЗС равна n = 4, то матрица будет иметь размер 4х4. Коэффициенты ХПЗС равны а4 = 2, а3 = 5, а2 = 10, а1 = 6, а0 = 1. Матрица имеет вид:
(обратите внимание на сходство строк матрицы: 1 с 3 и 2 с 4). Определители: Δ1 = 5 > 0,
Δ4 = 1* Δ3 = 1*209 > 0. Поскольку все определители положительны, то АСР устойчива. ♦ 3.1.5 Критерий Михайлова. Описанные выше критерии устойчивости не работают, если передаточная функция системы имеет запаздывание, то есть может быть записана в виде
где t - запаздывание. В этом случае характеристическое выражение замкнутой системы полиномом не является и его корни определить невозможно. Для определения устойчивости в данном случае используются частотные критерии Михайлова и Найквиста. Порядок применения критерия Михайлова: 1) Записывается характеристическое выражение замкнутой системы: Dз(s) = A(s) + B(s).e-ts. 2) Подставляется s = jw: Dз(jw) =Re(w) + Im(w). 3) Записывается уравнение годографа Михайлова Dз(jw) и строится кривая на комплексной плоскости.
Если годограф Михайлова проходит через начало координат, то говорят, что система находится на границе устойчивости.
3.1.6 Критерий Найквиста. Данный критерий аналогичен критерию Михайлова, но работает с АФХ системы, поэтому более сложен для расчетов. Последовательность: 1)
Определяется передаточная функция разомкнутой системы 2) Определяется число правых корней m. 3) Подставляется s = jw: W¥(jw). 4) Строится АФХ разомкнутой системы. Для устойчивости АСР необходимо и достаточно, чтобы при увеличении w от 0 до ¥ АФХ W¥(jw) m раз охватывала точку (-1; 0), где m - число правых корней разомкнутой системы.
В случае, если характеристическое уравнение разомкнутой системы A(s) = 0 корней не имеет (т.е. m = 0), то критерий, согласно критерию, замкнутая система является устойчивой, если АФХ разомкнутой системы W¥(jw) не охватывала точку (-1; 0), в противном случае система будет неустойчива (или на границе устойчивости). 3.2. Показатели качества Если исследуемая АСР устойчива, то может возникнуть вопрос о том, насколько качественно происходит регулирование в этой системе и удовлетворяет ли оно технологическим требованиям. На практике качество регулирования может быть определено визуально по графику переходной кривой, однако, имеются точные методы, дающие конкретные числовые значения. Показатели качества разбиты на 4 группы: 1) прямые - определяемые непосредственно по кривой переходного процесса, 2) корневые - определяемые по корням характеристического полинома, 3) частотные - по частотным характеристикам, 4) интегральные - получаемые путем интегрирования функций. 3.2.1 Прямые показатели качества. К ним относятся: степень затухания y, перерегулирование s, статическая ошибка ест, время регулирования tp и др.
Предположим, переходная кривая, снятая на объекте, имеет колебательный вид (см. рис. 1.38). Сразу по ней определяется установившееся значение выходной величины ууст. Степень затухания y определяется по формуле
где А1 и А3 - соответственно 1-я и 3-я амплитуды переходной кривой. Перерегулирование s = Статическая ошибка ест = х - ууст, где х - входная величина. Время достижения первого максимума tм определяется по графику. Время регулирования tp определяется следующим образом: Находится допустимое отклонение D = 5% ууст и строится «трубка» толщиной 2D. Время tp соответствует последней точке пересечения y(t) с данной границей. То есть время, когда колебания регулируемой величины перестают превышать 5 % от установившегося значения. 3.2.2 Корневые показатели качества. К ним относятся: степень колебательности m, степень устойчивости h и др. |
Copyright © 2012 г.
При использовании материалов - ссылка на сайт обязательна.
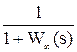 - по ошибке,
- по ошибке,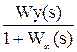 -
по возмущению.
-
по возмущению. Предположим,
что передаточная функция имеет вид
Предположим,
что передаточная функция имеет вид  x(t) =
Авхsin(wt) = sin(wt).
x(t) =
Авхsin(wt) = sin(wt).  АФХ - зависимость амплитуды и фазы от частоты
(изображается на комплексной плоскости);
АФХ - зависимость амплитуды и фазы от частоты
(изображается на комплексной плоскости);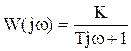 =
=
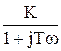 =
= 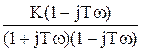 =
=
 Для
построения АЧХ и ФЧХ используются формулы:
Для
построения АЧХ и ФЧХ используются формулы: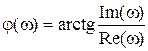 .
. Формула
для построения ЛАЧХ: L(w) = 20.lg Aвых(w).
Формула
для построения ЛАЧХ: L(w) = 20.lg Aвых(w).  ЛАЧХ ЛФЧХ
Пример цепи
ЛАЧХ ЛФЧХ
Пример цепи ЛАЧХ ЛФЧХ
Пример цепи
ЛАЧХ ЛФЧХ
Пример цепи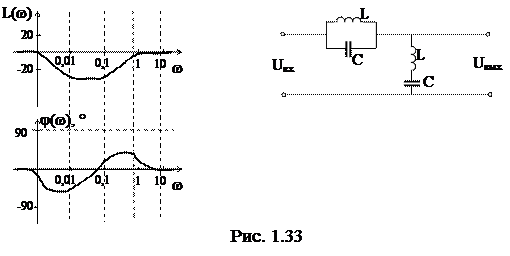
 Виды
корней характеристического уравнения:
Виды
корней характеристического уравнения: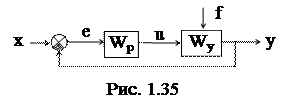 Wy -
передаточная функция объекта управления.
Wy -
передаточная функция объекта управления.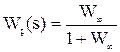 .
.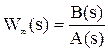 .
.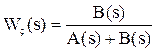 .
.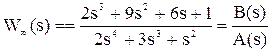 .
.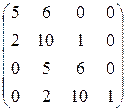
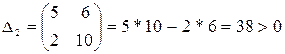 ,
,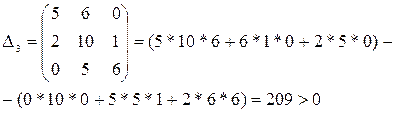
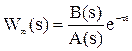 ,
, Для
устойчивой АСР необходимо и достаточно, чтобы годограф Михайлова (см. рис.),
начинаясь при w = 0 на положительной вещественной полуоси, обходил
последовательно в положительном направлении (против часовой стрелки) при
возрастании w от 0 до ¥ n
квадрантов, где n - степень характеристического полинома.
Для
устойчивой АСР необходимо и достаточно, чтобы годограф Михайлова (см. рис.),
начинаясь при w = 0 на положительной вещественной полуоси, обходил
последовательно в положительном направлении (против часовой стрелки) при
возрастании w от 0 до ¥ n
квадрантов, где n - степень характеристического полинома.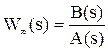 .
. Если
АФХ проходит через точку (-1; 0), то замкнутая система находится на границе
устойчивости.
Если
АФХ проходит через точку (-1; 0), то замкнутая система находится на границе
устойчивости.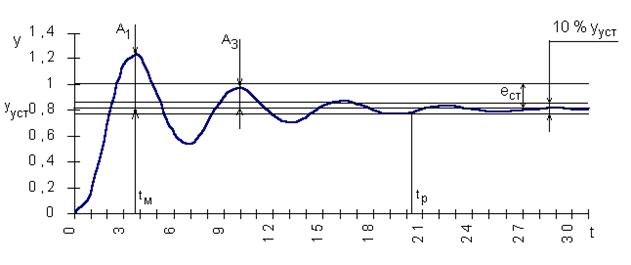
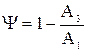 ,
,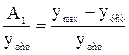 ,
где ymax - максимум переходной кривой.
,
где ymax - максимум переходной кривой.