Курсовая работа: Інтерполювання функцій
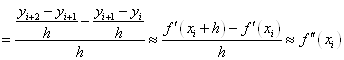 , ,
тобто 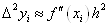 , і, взагалі, , і, взагалі, 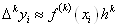 . (1.
2. 1) . (1.
2. 1)
Таким чином, на кінцеві різниці можна
дивитись як на деякий аналог похідних. Звідси справедливість багатьох їх властивостей,
однакових зі властивостями похідних.
Відмітимо лише найпростіші
властивості кінцевих різниць:
1.
кінцеві
різниці сталої дорівнюють нулю;
2.
сталий
множник у функції можна виносити за знак кінцевої різниці;
3.
кінцева
різниця від суми двох функцій дорівнює сумі їх кінцевих різниць в одній і тій
же точці.
Враховуючи роль, яку відіграють
многочлени в теорії інтерполювання, подивимось, що представляють собою кінцеві
різниці многочленна.
Так як многочлен в своїй канонічній
формі є лінійна комбінація степеневих функцій, покладемо спочатку 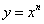 . Використовуючи
біноміальне розвинення п-ого степеня двочлена, отримаємо: . Використовуючи
біноміальне розвинення п-ого степеня двочлена, отримаємо:
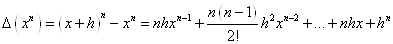
тобто перша кінцева різниця
степеневої функції 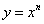 є многочлен степеня п-1 зі
старшим членом є многочлен степеня п-1 зі
старшим членом 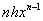 . Якщо взяти тепер кінцеву різницю
від функції . Якщо взяти тепер кінцеву різницю
від функції
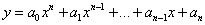 , (1. 2. 2) , (1. 2. 2)
то в силу лінійних властивостей 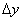 , можна записати , можна записати 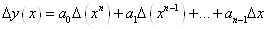 . Перший доданок в цій сумі, як
з’ясовано, є многочлен (п-1)-го степеня, другий, аналогічно, - многочлен
степеня п-2, і т. д. отже, перша кінцева різниця многочленна (1. 2. 2) в точці . Перший доданок в цій сумі, як
з’ясовано, є многочлен (п-1)-го степеня, другий, аналогічно, - многочлен
степеня п-2, і т. д. отже, перша кінцева різниця многочленна (1. 2. 2) в точці 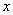 з короком з короком 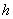 є многочлен зі старшим членом є многочлен зі старшим членом 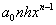 ,
друга кінцева різниця – многочлен зі старшим членом ,
друга кінцева різниця – многочлен зі старшим членом 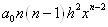 , …, , …, 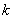 -та різниця –
многочлен зі старшим членом -та різниця –
многочлен зі старшим членом  . .
При 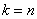 отримуємо постійну різницю п-го
порядку отримуємо постійну різницю п-го
порядку 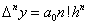 для многочлена (1. 2. 2), кінцеві
різниці більш високих порядків дорівнюють нулю. для многочлена (1. 2. 2), кінцеві
різниці більш високих порядків дорівнюють нулю.
Тобто, головний висновок із
попередніх роздумів: п-і кінцеві різниці многочленна п-ого степеня постійні, а
(п+1)-ші і всі наступні рівні нулю.
Однак, більш важливим для розуміння
суті поліноміального інтерполювання є твердження, обернене зробленому вище
висновку. А саме, що якщо кінцеві різниці п-го порядку деякої функції 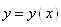 постійні
в будь-якій точці постійні
в будь-якій точці 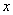 при різних фіксованих кроках при різних фіксованих кроках 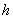 , то
ця функція , то
ця функція 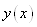 є многочлен степеня п. є многочлен степеня п.
Для функції 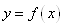 , заданої таблицею своїх
значень , заданої таблицею своїх
значень 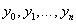 у вузлах у вузлах 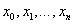 , де , де 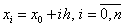 , кінцеві
різниці різних порядків зручно поміщати в одну загальну таблицю з вузлами і
значеннями функції. Цю загальну таблицю називають таблицею кінцевих різниць. , кінцеві
різниці різних порядків зручно поміщати в одну загальну таблицю з вузлами і
значеннями функції. Цю загальну таблицю називають таблицею кінцевих різниць.
1.2.1 Перша інтерполяційна формула
Ньютона
Нехай для функції 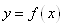 задані значення задані значення 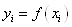 для рівновіддалених значень
незалежної змінної: для рівновіддалених значень
незалежної змінної: 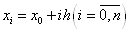 , де , де 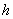 - крок інтерполяції. Необхідно
підібрати поліном - крок інтерполяції. Необхідно
підібрати поліном 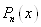 степені не вище п, який
приймає в точках степені не вище п, який
приймає в точках 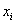 значення значення
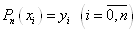 (1. 2. 3) (1. 2. 3)
Умови (1. 2. 3) еквівалентні тому, що 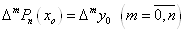 .
Слідуючи Ньютону, будемо шукати поліном у вигляді .
Слідуючи Ньютону, будемо шукати поліном у вигляді

Використовуючи загальний степінь,
вираз (1. 2. 3)
запишемо так:

Наша задача заклечається у визначенні
коефіцієнтів  полінома полінома 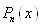 . Покладаючи . Покладаючи 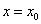 у вираз (1. 2. 5), отримаємо у вираз (1. 2. 5), отримаємо 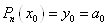 . .
Щоб знайти коефіцієнт 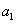 , складемо
першу кінцеву різницю , складемо
першу кінцеву різницю 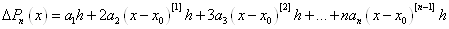 . Припускаючи в останньому виразі . Припускаючи в останньому виразі 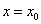 , отримаємо: , отримаємо: 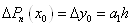 ; звідки ; звідки 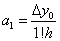 . Для визначення коефіцієнта . Для визначення коефіцієнта 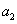 складемо кінцеву різницю другого
порядку складемо кінцеву різницю другого
порядку 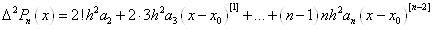 .
Покладаючи .
Покладаючи 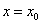 , отримаємо: , отримаємо: 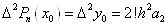 ; звідки ; звідки 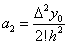 . Послідовно продовжуючи цей процес,
ми виявимо, що . Послідовно продовжуючи цей процес,
ми виявимо, що 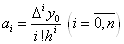 , де , де 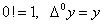 . .
Підставляючи знайдені значення
коефіцієнтів 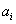 у вираз (1. 2. 5) отримаємо
інтерполяційний поліном Ньютона у вираз (1. 2. 5) отримаємо
інтерполяційний поліном Ньютона
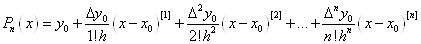 . (1. 2. 6) . (1. 2. 6)
Легко побачити, що поліном (1. 2. 6.)
повністю задовольняє вимогам поставленої задачі. Дійсно, по-перше, степінь
поліному 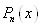 не вище п, по-друге, не вище п, по-друге, 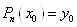 і і
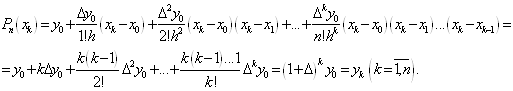
Замітимо, що при 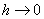 формула (1. 2.
6) перетворюється в ряд Тейлора для функції формула (1. 2.
6) перетворюється в ряд Тейлора для функції 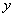 . Дійсно, . Дійсно,  Крім того, очевидно, Крім того, очевидно, 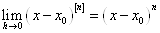 .
Звідси при .
Звідси при 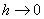 формула (1. 2. 6) приймає вид поліному
Тейлора: формула (1. 2. 6) приймає вид поліному
Тейлора:  . .
Для практичного використання
інтерполяційну формулу Ньютона (1. 2. 6) зазвичай записують в дещо
перетвореному вигляді. Для цього введемо нову змінну 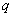 за формулою за формулою 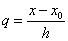 ; тоді ; тоді
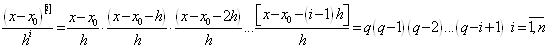
підставляючи ці вирази у формулу (1.
2. 6), отримаємо:
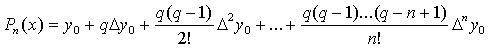 , (1. 2. 7) , (1. 2. 7)
де 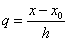 являє собою кількість кроків,
необхідних для досягнення точки являє собою кількість кроків,
необхідних для досягнення точки 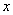 , виходячи із точки , виходячи із точки 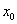 . Це і є
кінцевий вигляд першої інтерполяційної формули Ньютона. . Це і є
кінцевий вигляд першої інтерполяційної формули Ньютона.
Формулу (1. 2. 7) вигідно
використовувати для інтерполювання функції в околі початкового значення 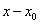 , де , де 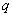 мале
за абсолютною величиною. мале
за абсолютною величиною.
Якщо у формулі (1. 2. 7) покласти
п=1, то отримаємо формулу лінійного інтерполювання: 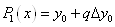 . При п=2 будемо мати формулу
параболічного або квадратичного інтерполювання . При п=2 будемо мати формулу
параболічного або квадратичного інтерполювання
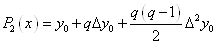 . .
Якщо дана необмежена таблиця значень 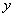 , то
число , то
число 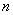 в інтерполяційній формулі (1. 2.
7) може бути довільним. Практично в цьому випадку число в інтерполяційній формулі (1. 2.
7) може бути довільним. Практично в цьому випадку число 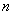 обирають так, щоб
різниця обирають так, щоб
різниця 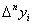 була постійною із заданою
точністю. За початкове значення була постійною із заданою
точністю. За початкове значення 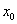 можна приймати довільне табличне
значення аргументу можна приймати довільне табличне
значення аргументу 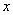 . .
Якщо таблиця значень функції
скінчена, то 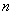 - число обмежене, а саме: - число обмежене, а саме: 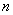 не
може бути більше числа значень функції не
може бути більше числа значень функції 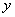 , зменшеного на одиницю. , зменшеного на одиницю.
Відзначимо, що при застосуванні
першої інтерполяційної формули Ньютона зручно використовувати горизонтальну
таблицю різниць, так як потрібні значення різниць функції знаходяться у
відповідному горизонтальному рядку таблиці.
1.2.2 Друга інтерполяційна
формула Ньютона
Перша інтерполяційна формула Ньютона
практично незручна для інтерполювання функції поблизу вузлів таблиці. В такому
випадку зазвичай застосовують другу інтерполяційну формулу Ньютона. Виведемо цю
формулу.
Нехай маємо систему значень функції 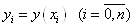 для
рівновіддалених значень аргументу для
рівновіддалених значень аргументу 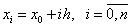 , де , де 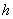 - крок інтерполяції.
Побудуємо поліном наступного вигляду: - крок інтерполяції.
Побудуємо поліном наступного вигляду:
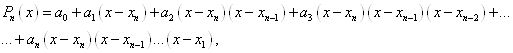
або, використовуючи узагальнену
степінь, отримуємо:
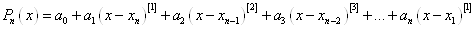 . (1. 2. 8) . (1. 2. 8)
Наша задача полягає у визначенні
коефіцієнтів 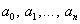 таким чином, щоб виконувались умови
(1. 2. 3). Для цього необхідно і достатньо, щоб таким чином, щоб виконувались умови
(1. 2. 3). Для цього необхідно і достатньо, щоб
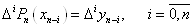 (1. 2. 9) (1. 2. 9)
Покладемо 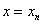 у формулі (1. 2. 8). Тоді будемо
мати: у формулі (1. 2. 8). Тоді будемо
мати: 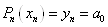 ,
отже ,
отже 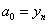 . .
Далі беремо від лівої і правої
формули (1. 2. 8) кінцеві різниці першого порядку
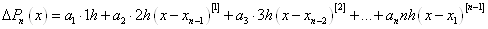 . .
Звідси, вважаючи 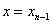 і враховуючи відношення
(1. 2. 9) будемо мати: і враховуючи відношення
(1. 2. 9) будемо мати:
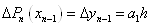 . Отже . Отже 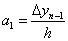 . .
Покладаючи 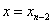 знаходимо: знаходимо: 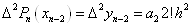 . І таким чином . І таким чином 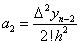 . .
Характер закономірності коефіцієнтів 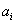 достатньо
зрозумілий. Застосовуючи метод математичної індукції, можна строго довести, що достатньо
зрозумілий. Застосовуючи метод математичної індукції, можна строго довести, що
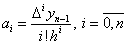 (1. 2. 10) (1. 2. 10)
Підставляючи ці значення у формулу (1.
2. 8) будемо мати остаточно
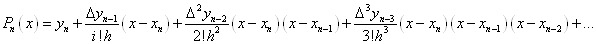 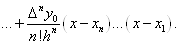 (1. 2. 11) (1. 2. 11)
Формула (1. 2. 11) носить назву другої
інтерполяційної формули Ньютона.
Введемо більш зручний запис формули (1.
2. 11). Нехай 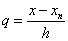 , тоді , тоді
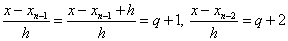 і т. д. і т. д.
Підставивши ці значення у формулу (1.
2. 11), отримаємо:
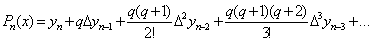 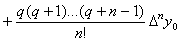 . (1.2.12) . (1.2.12)
Це і є загальний вигляд другої
інтерполяційної формули Ньютона. Для наближеного обчислення значень функції 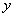 вважають,
що вважають,
що 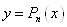 . .
Як перша, так и друга інтерполяційні
формули Ньютона можуть бути використані для екстраполяції, тобто, для
знаходження значень функції 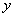 для значень аргументів для значень аргументів 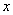 ,
котрі лежать за межами таблиці. Якщо ,
котрі лежать за межами таблиці. Якщо 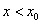 і і 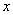 близько до близько до 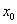 , то
вигідно використовувати першу інтерполяційну формулу Ньютона, причому тоді , то
вигідно використовувати першу інтерполяційну формулу Ньютона, причому тоді 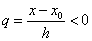 . Якщо
ж . Якщо
ж 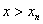 і і
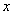 близько
до близько
до 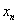 ,
то зручніше використовувати другу інтерполяційну формулу Ньютона, причому тоді ,
то зручніше використовувати другу інтерполяційну формулу Ньютона, причому тоді 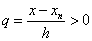 .
Таким чином, перша інтерполяційна формула Ньютона використовується для
інтерполяції вперед і екстраполяції назад, а друга інтерполяційна формула
Ньютона, навпаки, – для інтерполяції назад і екстраполяції вперед (див. [8]). .
Таким чином, перша інтерполяційна формула Ньютона використовується для
інтерполяції вперед і екстраполяції назад, а друга інтерполяційна формула
Ньютона, навпаки, – для інтерполяції назад і екстраполяції вперед (див. [8]).
Відмітимо, що операція екстраполяції,
взагалі кажучи, менш точна, ніж операція інтерполяції у вузькому значенні
слова.
1.2.3 Оцінка похибок
інтерполяційних формул Ньютона
Для функції 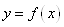 ми побудували
інтерполяційний поліном Ньютона ми побудували
інтерполяційний поліном Ньютона 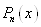 , який приймає в точках , який приймає в точках 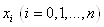 задані
значення задані
значення 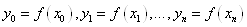 . Виникає питання, наскільки
близько побудований поліном наближається до функції . Виникає питання, наскільки
близько побудований поліном наближається до функції 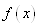 в інших точках, тобто
наскільки великий залишковий член в інших точках, тобто
наскільки великий залишковий член 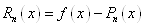 . Для визначення цього степеня наближення накладемо на функцію . Для визначення цього степеня наближення накладемо на функцію
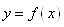 додаткові
обмеження. А саме, ми будемо припускати, що в області зміни додаткові
обмеження. А саме, ми будемо припускати, що в області зміни 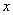 : : 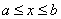 ,
котра містить вузли інтерполювання, функція ,
котра містить вузли інтерполювання, функція 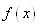 має всі похідні має всі похідні 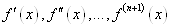 до (п+1)-го порядку
включаючи. до (п+1)-го порядку
включаючи.
Введемо допоміжну функцію
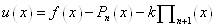 , (1. 2. 12) де , (1. 2. 12) де 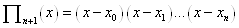 і і
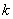 - постійний коефіцієнт, котрий буде
обрано нижче. - постійний коефіцієнт, котрий буде
обрано нижче.
Функція 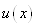 , очевидно, має п+1 корінь в точках , очевидно, має п+1 корінь в точках 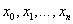 . Підберемо тепер коефіцієнт . Підберемо тепер коефіцієнт 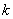 таким
чином, щоб таким
чином, щоб 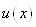 мала (п+2)-ий корінь в будь-якій,
але фіксованій точці відрізка мала (п+2)-ий корінь в будь-якій,
але фіксованій точці відрізка 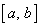 , яка не співпадає з вузлами
інтерполювання (мал. 1). Для цього достатньо покласти , яка не співпадає з вузлами
інтерполювання (мал. 1). Для цього достатньо покласти
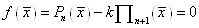 . .
Звідси, так як 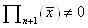 , то , то
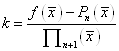 (1. 2. 13) (1. 2. 13)
При цьому значення множника 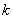 функції функції 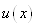 має п+2 кореня на
відрізку має п+2 кореня на
відрізку 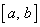 і буде обертатись в нуль на
кінцях кожного з відрізків і буде обертатись в нуль на
кінцях кожного з відрізків
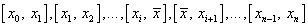 . Застосовуючи теорему Ролля [11] до кожного із цих відрізків,
переконуємось, що похідна . Застосовуючи теорему Ролля [11] до кожного із цих відрізків,
переконуємось, що похідна 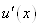 має не менше п+1 кореня на
відрізку має не менше п+1 кореня на
відрізку 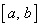 . .
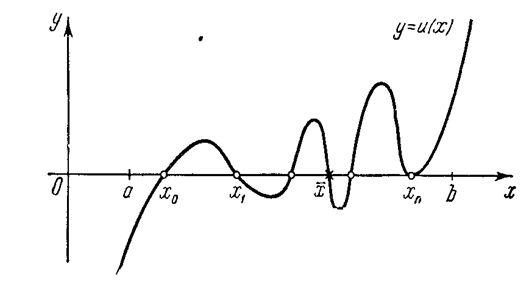
Малюнок 1. Графік функції 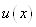
Застосовуючи теорему Ролля до
похідної 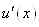 , ми
переконаємося, що друга похідна , ми
переконаємося, що друга похідна 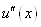 перетворюється в нуль не менше п
разів на відрізку перетворюється в нуль не менше п
разів на відрізку 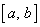 . .
Продовжуючи ці роздуми, прийдемо до
висновку, що на відрізку 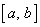 похідна похідна 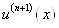 має хоча б один корінь,
котрий позначимо через має хоча б один корінь,
котрий позначимо через 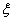 , тобто , тобто 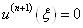 . .
Із формули (1. 2. 11) так як  , маємо: , маємо: 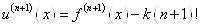 . При . При 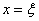 , отримуємо: , отримуємо: 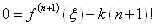 Звідси Звідси
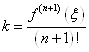 .
(1. 2. 14) .
(1. 2. 14)
Порівнюючи праві частини формул (1. 2. 13) і (1. 2. 14), будемо мати:
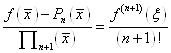 , тобто , тобто
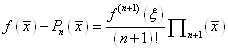 . (1. 2. 15) . (1. 2. 15)
Так як 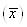 довільне, то формулу (1. 2. 15) можна записати і так: довільне, то формулу (1. 2. 15) можна записати і так:
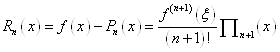 , (1. 2. 16) , (1. 2. 16)
де 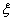 залежить від залежить від 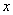 і лежить всередині відрізка і лежить всередині відрізка 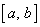 . .
Страницы: 1, 2, 3, 4, 5
|

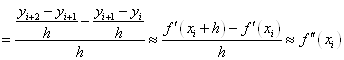 ,
, 
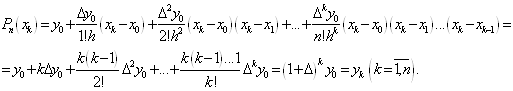
 Крім того, очевидно,
Крім того, очевидно, 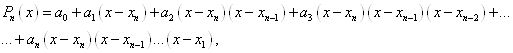
 (1. 2. 13)
(1. 2. 13)
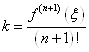 .
(1. 2. 14)
.
(1. 2. 14)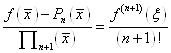 , тобто
, тобто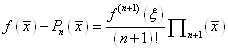 . (1. 2. 15)
. (1. 2. 15)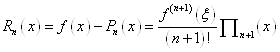 , (1. 2. 16)
, (1. 2. 16)