 |
|
МЕНЮ
|
Курсовая работа: Інтерполювання функційВідмітимо, що формула (1. 2. 16) справедлива для всіх точок
відрізка На основі формули (1. 2. 16) отримаємо залишковий член першої інтерполяційної формули Ньютона:
де Аналогічно, покладаючи в формулі (1. 2. 17)
де Зазвичай при практичних обчисленнях інтерполяційна формула Ньютона обривається на членах, що містять такі різниці, які в межах заданої точності можна вважати постійними. Вважаючи, що
В цьому випадку залишковий член першої інтерполяційної формули Ньютона наближено рівний
При таких самих умовах для залишкового члена другої інтерполяційної формули Ньютона отримаємо вираз
1.3 Інтерполяційні формули Гауса При побудові інтерполяційних формул Ньютона використовуються лише значення функції, що лежать з однієї сторони початкового наближення, тобто, ці формули носять односторонній характер (див.[3]). В багатьох випадках виявляються
корисними інтерполяційні формули, що містять як наступні, так і попередні
значення функції по відношенню до її початкового наближеного значення. Найбільш
вживаними серед них являються ті, що містять різниці, розміщені у
горизонтальному рядку діагональної таблиці різниць даної функції, що відповідає
початковим значенням Відповідні їм формули називають інтерполяційними формулами із центральними різницями. До їх числа відносяться формули Гауса, Стірлінга і Бесселя. Постановка задачі. Нехай маємо 2п+1 рівновіддалені вузли інтерполяції:
де
для всіх відповідних значень і та k. Будемо шукати поліном у вигляді:
Вводячи узагальнені степені (див [3]), отримаємо:
Застосовуючи для обчислення
коефіцієнтів
Далі вводячи змінну
або, коротше,
де Перша інтерполяційна формула Гауса містить центральні різниці
Аналогічно можна отримати другу
інтерполяційну формулу Гауса, котра містить центральні різниці
або, в скорочених позначеннях,
де Формули Гауса застосовуються для
інтерполювання в середині таблиці поблизу 1.4 Інтерполяційна формула Бесселя Для того, щоб вивести формулу Бесселя використаємо другу інтерполяційну формулу Гауса (1. 3. 6). Візьмемо Якщо обрати за початкове значення
прикладний задача інтерполяційний формула Візьмемо тепер за початкове значення
Взявши середнє арифметичне формул (1. 4. 1) і (1. 4. 2), після нескладних перетворень отримаємо інтерполяційну формулу Бесселя:
де Тобто, інтерполяційна формула Бесселя
(1. 4. 3), як слідує із способу отримання її, представляє собою поліном, який
співпадає з даною функцією В окремому випадку, при п=1, нехтуючи
різницею
або У формулі Бесселя всі члени, котрі
містять різниці непарного порядку, мають множник
Цей спеціальний випадок формули Бесселя
називається формулою інтерполювання на середину. Якщо у формулі (1. 4. 3)
зробити заміну змінної за формулою
де Формула Бесселя використовується для
інтерполювання всередині таблиці при значеннях q, близьких до 0.5. Практично
вона використовується при 1.5 Інтерполяційна формула Стірлінга Якщо взяти середнє арифметичне першої інтерполяційної формули Гауса (1. 3. 4) та другої формули Гауса (1. 3. 6), то отримаємо формулу Стірлінга:
де Легко бачити, що Формула Стірлінга використовується
для інтерполювання в середині таблиці при значеннях 1.6 Оцінки похибок центральних інтерполяційних формул Приведемо залишкові члени для формул Гауса, Стірлінга і Бесселя [12]. 1. Залишковий член інтерполяційних формул Гауса (1. 3. 4) і (1. 3. 6) та інтерполяційної формули Стірлінга (1. 5. 1). Якщо 2п – порядок максимальної різниці таблиці, яка використовується і де Якщо ж аналітичний вираз функції 2. Залишковий член інтерполяційної формули Бесселя (1. 4. 3). Якщо 2п+1 – порядок максимальної
використовуваної різниці таблиці і
де Якщо ж функція
Найбільш простий вигляд формула має при q=0.5, так як всі члени, що містять різниці непарного порядку зникають. Цей спеціальний випадок формули Бесселя називається формулою інтерполювання на середину. Її використовують для ущільнення таблиць [4], тобто для складання таблиць з більш малим кроком. Для залишкового члена при q=0.5 маємо:
1.7 Інтерполяційна формула Ньютона для нерівновіддалених вузлів Для побудови інтерполяційних формул у
випадку довільного розташування упорядкованих не співпадаючих вузлів Через значення функції
На різницях (1. 7. 1) шукаються розділені різниці другого порядку:
і т.д. Таким чином, якщо визначені
k-ті різницеві відношення
Нехай
Для розділеної різниці другого
порядку по точкам
Формально, на основі рекурентного
відношення (1. 7. 2) цей процес може бути продовжений. В результаті можна
записати формулу, яка описує своєрідне розкладання
Якщо
Припустимо, що цей многочлен
Підставивши
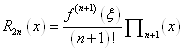
другий доданок якої може розглядатись в якості залишкового члена, тобто
де Так як для обчислення різниці При практичному використання
інтерполяційної формули (1. 7. 5) доводиться покладатися на зменшення модулів доданків 1.8 Приклади застосування інтерполяційних формул 1.8.1 Приклад 1 Використовуючи першу і другу
інтерполяційну формулу Ньютона і Гауса, а також інтерполяційні формули
Стірлінга і Бесселя необхідно знайти значення функції Таблиця 1. Значення функції
Розв’язання: |
Copyright © 2012 г.
При использовании материалов - ссылка на сайт обязательна.


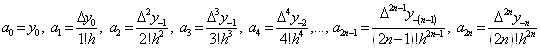





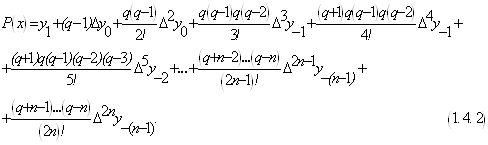
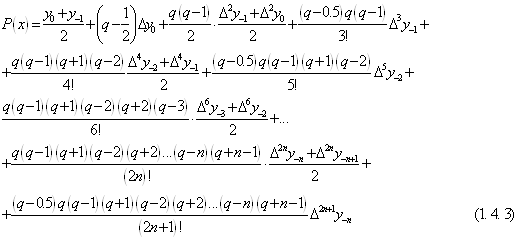



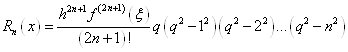 ,
, 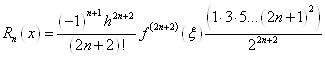 .
.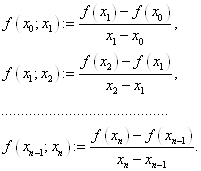 (1. 7. 1)
(1. 7. 1)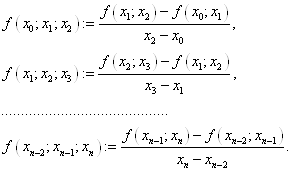
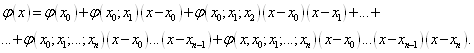 (1. 7. 4)
(1. 7. 4)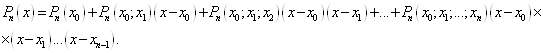

 .
.